728x90
반응형
Q. 두 수를 입력받아 거듭제곱을 리턴해야 합니다.
power이라는 함수에 지수를 나타내는 base, 연산해야 하는 번수를 나타내는 exponent가 인자로 들어온다
- 시간 복잡도 고려하지 않고 구현한 코드
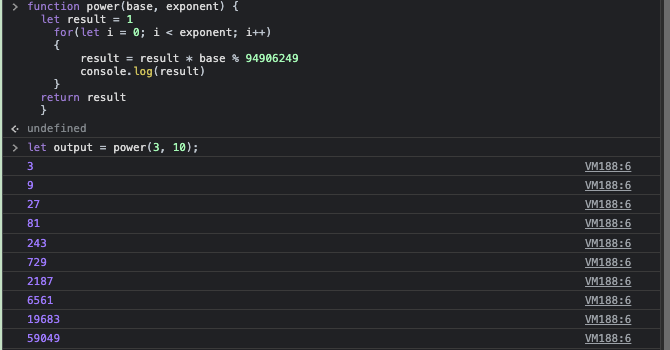
function power(base, exponent) {
let result = 1
for(let i = 0; i < exponent; i++)
{
result = result * base % 94906249
}
return result
}이 코드는 효율적이지는 않지만 간략하게 구현할 수 있다
result의 값을 base로 곱해주고 result에 넣어주면 된다.
result를 구할 때마다 나누기 94,906,249를 해주는 이유는 컴퓨터가 나타낼 수 있는 값으로 표현해주기 위해서이다.
power에 3과 10을 인자로 넣는다면 3을 10번 곱해서 원하는 값을 도출해낸다
하지만 exponent에 1000을 넣는다면 컴퓨터는 1000번의 연산을 해야할 것이다.
728x90
- 시간 복잡도 고려한 코드
function power(base, exponent) {
if (exponent === 0) return 1;
const half = parseInt(exponent / 2);
const temp = power(base, half);
const result = (temp * temp) % 94906249;
if (exponent % 2 === 1) return (base * result) % 94906249;
else return result;
}이 코드는 먼저 exponent를 2로 나누는 과정을 재귀함수를 통해 계산한다.
그리고 parseInt를 이용해 정수로 만드는 과정이 들어가기 때문에 exponent가 홀 수 일 경우 계산을 한 번 더 해주는 과정을 거친다

계산되어가는 과정은 이렇다
아까와 같이 exponent에 10의 숫자가 들어갔는데 계산과정은 4번으로 줄어든다.
이렇게 문제 하나를 작은 문제로 분할하여 해결하는 것을 분할정복(Divide conquer)이라고 한다.
분할 정복을 이용하여 구하니 10,000,000까지도 빠르게 계산되는 모습을 보였다
728x90
반응형
'junior developer :) > 알고리즘 & 코딩테스트' 카테고리의 다른 글
| [알고리즘]삽입정렬(Insertion Sort)_JS (0) | 2022.12.06 |
|---|---|
| 이진탐색(binary search)_반복문과 재귀함수를 통한 풀이 (0) | 2022.11.29 |
| 알고리즘_깊이우선탐색(DFS),너비우선탐색(BFS) / JS (2) | 2022.11.05 |
| [알고리즘]오름차순으로 정렬하기_JS(버블정렬, 선택정렬) (0) | 2022.11.01 |
| 알고리즘_ fibonacci 수열 구현하기 (JS/시간복잡도에 따른 두가지 구현 방식 비교) (0) | 2022.10.25 |


